Kao sto znamo foton je definisan kao osnovni kvant energije, pri cemu je dualisticka priroda svetlosti nesporna. Ono sto je pri tome paradoksalno je cinjenica da foton nazivamo cesticom a u potpunosti ga tretiramo kao talas. Ako se pazljivo prouce eksperimenti radjeni sa optickim talasima, lako se moze uociti da dosledno postovanje principa dualizma, naucno - priznatog svim energetskim aspektima egzistencije materije, u slucaju fotona jednostavno nije ispostovano (osim samo deklarativno).
 Komptonov efekat, pojava pri kojoj se sasvim jasno manifestuje korpuskularna priroda elektromagnetnog zracenja, POTPUNO JE NEPRIMENJIVA na opticke talase !
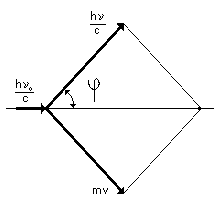
Komptonov efekat, pojava pri kojoj se sasvim jasno manifestuje korpuskularna priroda elektromagnetnog zracenja, POTPUNO JE NEPRIMENJIVA na opticke talase !Naime, Kompton je proucavao pojavu da se u snopu monohromatskog X-zracenja, koje prolazi kroz foliju od nekog metala, posle rasejavanja nalaze i zraci nesto vece talasne duzine, odnosno manje energije. Tumacenje je dao jos 1922.godine. Cinjenicu da se u snopu monohromatskog zracenja, nakon prolaska kroz foliju mogu naci i talasi sa nesto manjom energijom, objasnio je kao posledicu sudara dveju cestica: fotona (X-zraka) i elektrona u foliji. Kompton je posao od pretpostavke da X-zracenje ima i cesticnu prirodu i da se, opisno receno, ponasa isto kao sto se ponasa i npr. bilijarska kuglica koja se sudara sa drugom kuglicom sa elektronom.
SUSTINSKA nedefinisanost koja je zaobidjena, kako onda tako i danas, je CIME to foton deluje na elektron -, jer materija bez mase NEMOZE posedovati tromo teske kvalitete (osobine u gravitaciono-kinematickom smislu), pa priroda interakcije postaje, najblaze receno, paradoksalna. No ...
Bilo kako bilo, Kompton je pokazao da promena frekvencije fotona (TALAS!) zavisi od ugla pod kojim foton skrece posle sudara (?) sa elektronom (CESTICA!). Njegov obrazac:
d l = 0,048*10-10 sin2 (f / 2)
dobro se slagao sa eksperimentalnim rezultatima (za f = 0 i dl = 0, tj. ako se foton ne rasejava, nema ni promene energije (talasne duzine odnosne boje. Isto tako, za f = p, imamo maksimalno slabljenje fotona: dl = 0.048*10-10 m, sto je u slucaju sudara X-zraka i elektrona eksperimentalno verifikovano sa zadovoljavajucom tacnoscu) … cime je potvrdjeno da se elektromagnetnom zracenju mogu pripisati i korpuskularna svojstva ... l = 4.8*10-7 + 0.048*10-10 = 4.800048*10-7 m,
odnosno neznatno (za svega stohiljaditi deo svoje vrednosti) uvecanu talasnu duzinu, sto bi znacilo da je, nakon direktnog, ceonog sudara njegova energija gotovo neumanjena, odnosno BOJA SASVIM NEPROMENJENA, sto prakticno, jednostavno NIJE TACNO. d l = 2.76*10-4 sin2 (f / 2).
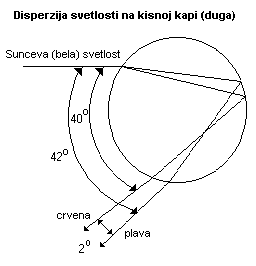
Proverimo ga u praksi. Razlika talasnih duzina plave i crvene boje (plava: 4.8*10-7 m i crvena: 6.5*10-7 m) iznosi 1.7*10-7 m, sto mozemo shvatiti kao dl, pa iz gornjeg obrasca dobijamo f = 2,8o, sto se IZVANREDNO slaze sa realnoscu jer je poznato da npr. kod duge, ugao izmedju crvene i plave komponente sunceve svetlosti iznosi 2o (usled nejednakog prelamanja bele sunceve - svetlosti, na kisnim kapima, javlja se ugao izmedju crvene i plave komponente svetlosnog spektra).
Cinjenica da je ovaj obrazac POTPUNO NEPRIMENJIV na oblast optickih talasa, precutana je do danasnjeg dana. Ipak i opticki talasi su deo elektromagnetnog spektra, pa pogledajmo sta dobijamo za slucaj fotona (npr. plave boje tj. talasne duzine 4.8*10-7 m) koji nakon direktnog sudara ima talasnu duzinu uvecanu za dl (max):
Kako onda STRUKTURNO objasniti npr. mehanizme difrakcije elektromagnetnih talasa iz optickog spektra?
U praksi se to radi primenom tzv. indeksa loma, vezanog za pojam gustine (pri tome se podrazumeva OPTICKA a ne mehanicka gustina), pri cemu se mehanizam delovanja te iste sredine na opticki foton POTPUNO zaobilazi, vesto uklopljenim objasnjenjima u kojima se koristi tzv. Hajgensov princip, zasnovan na talasnoj prirodi interagujucih objekata ...
Bilo kakva korekcija komptonovog obrasca za njegovu primenu na opticki deo (inace sasvim kontinuiranog) elektromagnetnog spektra je nemoguca iz prostog razloga sto koristenje principa ekvivalencije (de Broglieve relacije) podrazumeva prethodno definisanje sasvim odredjene vrednosti talasne duzine (na osnovu koje onda dobijamo odgovarajucu masu) iz optickog dela spektra relativno sirokog opsega talasnih duzina. Na pitanje: Koja bi to eksplicitna vrednost mogla biti?, savremena nauka NEMA odgovor!
 Sa aspekta modela KGE odgovor je vrlo jednostavan. Naime, po ovom modelu foton, kao (svaka prava) cestica IMA SAVIM REALNU MASU mirovanja od: m = 1.6*10-38 kg, pa Komptonov obrazac, za slucaj optickih talasa, dobija vrednost:
Sa aspekta modela KGE odgovor je vrlo jednostavan. Naime, po ovom modelu foton, kao (svaka prava) cestica IMA SAVIM REALNU MASU mirovanja od: m = 1.6*10-38 kg, pa Komptonov obrazac, za slucaj optickih talasa, dobija vrednost:
Primenom klasicnog komptonovog obrasca na vrednost ugla f od 2o, koji se u praksi veoma lako meri, dobija se odgovarajuca ocekujuca promena frekvencije od dl = 1.46*10-11 m, sto je netacno za vise redova velicine, jer je dl stvarno = 1.7*10-7 m, dok je odstupanje po modelu KGE zaista sasvim zanemarivo ...
Imajuci u vidu veoma dobro slaganje eksperimentalnih rezultata (obrazac se moze proveriti i za druge vrednosti uglova boja, kao i za eksperimente sa prizmom…) sa onima koje predvidja model KGE, kao i cinjenicu da se svetlosnim, a time i optickim, talasima pridruzuje klasicna, korpuskularna struktura koja je sasvim analogna npr. kosmickim zracima, cime im se vraca atribut normalnih elektromagnetnih talasa, sada lako i POTPUNO SHVATLJIVE dualisticke prirode, ideju o postojanju realne mase mirovanja fotona mozemo smatrati u potpunosti opravdanom, pogotovo sto svi obrasci (klasicne, relativisticke i kvantne) fizike ostaju prakticno neizmenjeni a sve postojece teorije i dalje vazece.