VELOCITY OF LIGHT
15./july/2003
Author: Dane Gacesa
ABSTRACT
a)
Light source (macrosource) is a set of
elementary sources which have different velocities in relation to inertial
frame of the macrosource.
Elementary light which is emitted by an
elementary source has a strictly fixed speed c in relation to that elementary
source in the moment of emission.
Hereby follows that the
macrosource is emitting lights that have different speeds in relation to its
own inertial frame.
b)
Elementary light detector can
only detect the light that in relation to it has speed c. Just that kind of light is detectable in the inertial frame of
the elementary detector.
c)
The constancy of speed of
light is only related to the detectable light and it is exclusivly the
consequence of the strict detectors
selectivity.
Change of relative velocity
between the light source and the detector can`t effect the detectors
selectivity therefore the light speed that we detect in the inertial detectors
frame is always the same. But every time
another light is detectable depending on that relative velocity.
CONTENTS
In all of the experiments for determining the speed of light depending on the relative uniform motion between the source and the observer, the mandatory participants are:
- the light (electromagnetic waves) and,
- the light detector;
The results
of these experiments could be the consequence of the property that belongs to
the light, or the consequence of the property that belongs to the detector.
This other possibility was not ever analyzed in the domain of modern Science.
Without any doubt, it is a roughly overlooked
matter, which must not be neglected in the strict scientific analysis of the
experimental results.
The
experimenters that were researching the dependence of the speed of light from
the relative uniform motion between the source and the observer never asked
themselves: how we could detect the light whose speed depends on such a
motion; that is, a light that would not have a speed c in relation to the
observer, that is, by which devices they could detect the light that would not
be electromagnetic in nature?
Electromagnetic waves are spreading by the strictly determined speed c,
in the relation to the source of these waves. The light is also spreading with
that speed and it is the part of the electromagnetic spectrum. Thus, the speed
c is an essential characteristic of the electromagnetic waves – which means
that the waves spreading at the different speed than the speed c are not
electromagnetic.
Thus,
there is a chance that the lights with a different speed than the speed c were
not detected not only because such lights do not exist, but because they could
not have been detected. However, those lights could exist and could be detected
when the relative speed c is achieved
between any one of them and the detector.
If the
light source emits even the lights that in relation to the source have
different speeds than the speed c, being that the speeds are also mutually
different, then the detector should be strictly selective, and more exactly it
should interact with only one from them in order that the source information is
clear and not blended.
The
experimental fact is that the detector interacts with only such a light that in relation to it has the speed c, in
other words when certain light in relation to it has a speed c. The detector
could interact with any light emitted by the source with the condition of
achievement of the speed c between that light and the detector. Then, such a
light is electromagnetic in nature in the detector’s inertial frame, and more
exactly, then – such light is detectable. Because the detector could move at
any relative velocity (within determined borders) in relation to the source
there follows that there is always certain light that in relation to the
detector’s inertial system has the speed c with which the detector interacts.
“The Constancy of the speed of
light” is the consequence of the strict detector’s selectivity. The
speed of light is directly dependent on the relative speed between the source
and the observer, but the light is detectable only when its speed is equal to
c, in the relation to the detector.
Thus, it is
obvious, that it was highly illusory to expect that by the help of any
experiment it could be possible to detect the light that has a different speed
from the value c.
If the
light source, in fact, emits the lights with different speeds then it is
necessary to single out certain interval of these lights with already known
borderline speeds and then it should be experimented with this interval and not
with the total emission of such a source.
It is possible to achieve such a selection. The experiments with the lights from this
interval are fundamentally different from the experiments already conducted.
The suggested experiments, in this text, could unmistakably give an answer to
the question why the speed of the (detectable!) light does not depend on the
relative speed between the source and the observer.
INTRODUCTION
The light velocity is a characteristic of light that has not been thoroughly researched. An error was made in the interpretation of experiments that had the following aim – establishing of the value of light velocity depending on the relative motion between a light source and an observer. The assumptions and expectations of an experimenter could be briefly described in a following way:
1. It
was expected that the light would have lower velocity in its relation to
observer, if the light source and the observer were moving away from each other
and vice versa.
2. The
attention was not given to the nature of such a light, in other words to the
nature of light that would have lower or higher velocity than what the actual
velocity of electromagnetic waves (c) was, in its relation to observer.
3. It
was assumed that an eye or the other light detector would have the ability to
detect even such light.
4. Because
such light was not detected, it was determined that it does not exist!
Several
natural phenomena are taking part in each experiment. The result of the interaction
of characteristics of these phenomena is independent of the goal that the
experimenter is trying to achieve, and hence - it is necessary to consider the
principle of the research of characteristics distinctive to all phenomena
taking part within the experiment. Let’s analyze in this sense, all of
the four given conclusions:
Ad 1. This
expectation is normal because it is in accordance with an experience.
Ad 2. The
light with lower, or higher velocity of actual velocity c, would not be
electromagnetic in nature in its relation
to
observer.
Ad 3.
Here, without doubt, an error was made in principle. Ad hoc characteristic
was given to an eye, or to the electromagnetic waves’ detectors.
The detector does not have and
could not have this characteristic because in such case, the detector would
stand for a device able to achieve interaction even with non-electromagnetic
waves, in other words – detector would be able to interact with two
phenomenally different types of waves. In such case, the information would be
unclear, mixed up or even impossible.
And, that by itself is the case why we have to have strictly selective
light detector. The light detection device detects only specific light that in
relation to it (light detector) has the speed c.
Ad 4. In
the meantime, a strict selectivity of the detector does not exclude possibility
of existence of the waves that have different velocity and not the velocity c.
Therefore,
the light source could emit other lights with velocities different from the
velocity c, but those lights cannot be detected until relative velocity c is
reached between any one of them and the detector. (If for example, the source of light emits
the light which in its relation to the source has the velocity: c + 5 km/sec., then the detector (an
observer) should be moving away from the source at a velocity v = 5km/sec in
order to achieve the relative velocity c between that light and the detector; in other words: in order to achieve interaction between that
light (now electromagnetic in nature) and the detector. This is, of course,
true for the light velocities lower than the value c – when a detector should
be moving to the source at the appropriate velocity).
From these conclusions
results the following
Hypothesis
1. The
light source emits limited set of light spectra spreading at various velocities
in the relation to the source’s inertial system.*
2. Any
light spectrum could be detected only in the particular inertial system and it
has to have velocity c in its relation to it. At that time, that spectrum is
the electromagnetic spectrum in that inertial system.
3. Relative
velocity of the light spectrum in its relation to the observer is equal to the
vector related difference of the velocities of both, light spectrum and the
observer in their relation to the referential system.*
A term
“light spectrum” is used because the Hypothesis supports the following: the
spectrum (as a part of the whole spectrum) could be electromagnetic and non-electromagnetic.
Under the term “light”, we usually mean detectable light spectrum
(electromagnetic). The velocity of the entire spectrum (that could also be
electromagnetic and non-electromagnetic) is the same as the velocity of its
part (light spectrum).This Hypothesis is not opposed to the Maxwell
electro-dynamics because it does not treat spectra of non-electromagnetic
nature, but it is opposed to the Special Theory of Relativity for it does not
accept light speed constancy. The Second Postulate of the Special Theory of
Relativity according to this Hypothesis, should be formulated in the following
way:
Relative speed of light we could detect does not depend on relative uniform
movement between the source and the observer. According
to this hypothesis, if the observer is moving with any relative uniform speed
in the relation to the source, here will always exist certain light spectrum in
its inertial system whose velocity satisfies the requirement of its detection.
* inertial system = inertial frame
* referential system = reference frame
Light emission
Light
source (macro source) is the final set of elementary sources that are
intensively moving at various speeds in their relation to the inertial system
of the macro source and this is due to the incoming energy. Those speeds ve form a
speed set limited by the extreme speed values of the elementary sources:
ve min < ve <
ve max
1
At a
certain moment, at any elementary source speed ve,
elementary source could emit the elementary light. In the moment of emission,
elementary light has the speed c in its relation to the instantaneous inertial
system of elementary source, and speed c + ve in
its relation to the inertial system of the macro source. Thus, the lights emitted by the macro source have
various speeds vs in the set of speeds defined by the maximal and
minimal elementary source velocity. If we adopt the direction of light in its
relation to the source as a positive one, then we have:
c + ve min < vs <
c + ve max
2
where, ve min and ve
max are the extreme speed values of elementary sources, and vs are
the velocities of light spectra in their relation to the inertial system of
macro source (pic. 1).
The set (1) is a final one, and it has as
many members as there are different active elementary sources’ speeds in a
specific moment. Elementary sources with same speeds at the time of emitting
elementary light, represent a sub-set emitting light spectrum of speed :
vs = c + ve
3
Every set member is the sub-set
of the particular speed in its relation to the inertial system of the macro
source whose speed differs from the speeds of other sub-sets. In the next
moment, new set is «formed» in the macro source with its sub-sets that are
different than the previous ones, but are within the same borders. Sets'
shifting is highly intensive and thus is created the impression of a macro
source emitting light in every moment with all possible speeds from the
interval (2).
If we could imagine a
fictitious macro source emitting complete electromagnetic spectrum in its
inertial system altogether with other complete non-electromagnetic spectra,
then all conclusions about light spectra are related to such source (complete
spectra) as well.
GRAPHIC VIEW OF THE LIGHT
EMISSION
VS = C + Ve
vs



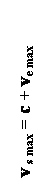
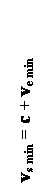
![]()
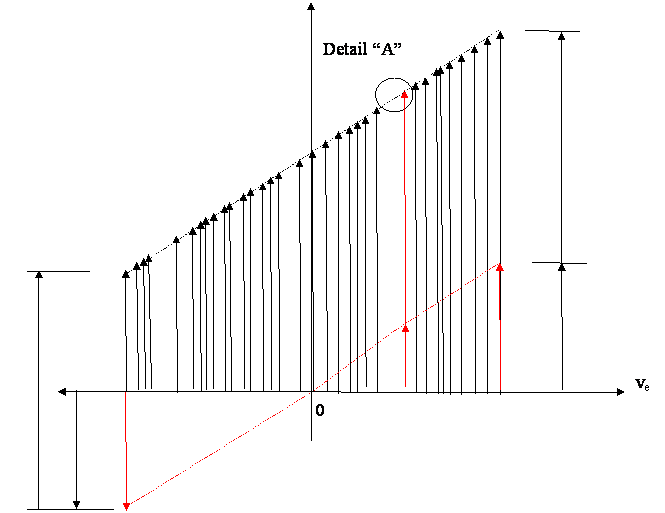
Pic. 1
Detection
Spectrum (3) could be detected in
such inertial system in which such spectrum has the velocity c, in other words
speed vr of such inertial
system in its relation to the inertial system of macro source must satisfy
condition
vs - vr = c
4
This is the requirement for a
detection achievement. Because vs = c + ve, it follows that
vr = ve
5
which means that the detector in this case must be in the same inertial system as the elementary source was during emission. By changing ve into vr in the expression (1), we are going to get a set
ve min < vr < ve
max 6
If the observer's
(detector's) velocity in relation to the macro source is outside of such
set, interaction between any spectrum
emitted by the source and the detector is not going to be possible because such
source does not emit spectrum which is possible to detect in such case in the
observer's inertial system. Thus, the extreme velocities of the spectra yet
possible to be detected are vs min = c + ve min, and vs max = c + ve max.
The light
could be detected from any inertial system in the set (6), but the group (6)
contains an infinite number of inertials systems, so it appears as macro source
should emit an infinite number of spectra, so to speak, one spectrum of
appropriate
speed for each inertial system, or otherwise macro
source ought to radiate with infitely great energy, or with final amount of
energy necessary to be divided over infinite number of inertial systems.
Naturally, neither one, nor the other is possible. However, it comes out that
it is not even necessary !
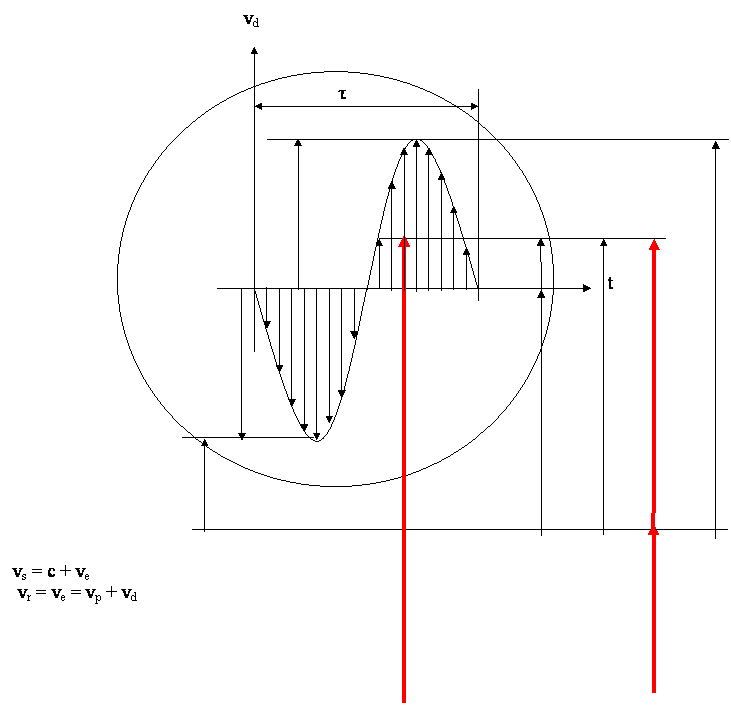
The
macrodetector is also a set of elementary detectors that are moving (vibrating)
at various speeds vd in their
relation to the macrodetectors inertial system. Those speeds are of much lower
intensity than those speeds of the elementary sources. The assemblage of these
speeds is limited by the extreme speeds, and so we have got
vd min <
vd < vd max 7
No matter how small the difference between the extreme
speeds of such set, it contains an infinite number of various speeds taken over
by the elementary detector during only one vibration. If macrodetector (an
observer) is positioned within the inertial system which in relation to the
macro source’s inertial system has a velocity vp, then the
elementary detector is within certain moment positioned in the inertial system
with velocity vr = vp + vd in relation to the macro source’s inertial
system.
By exchanging the signs in the expression
(4) we get
vs - vp - vd = c
8
Elementary detector takes over all speeds vd
between the speeds vd min and vd max in the very short period of time, so it is
sufficient that macro source emits any
one and only one spectrum from
the interval of speeds
c + vp + vd min < vs < c + vp + vd
max 9
at least for that much time that is needed for one
elementary detector's vibration to last (pic. 2), so thus will that spectrum be
detected in the moment when the elementary detector reaches such velocity vd so that the requirement (8) is met. Thus, the
entire set (9) containing infinite number of speeds could be
« covered » only with one spectrum and any one spectrum whose speed
meets the requirement (8). Hence, the observer (macrodetector)
could detect any spectrum from an interval (9) not violating in any way the
detection requirement (4), because it is strictly valid at the elementary level
(8).
The set (2) contains final number of sets
(9) and out of that fact there follows the conclusion : macro source
should not emit infinite number of spectra, and more exactly, infinitely great
energy although we can detect light from infinite number of inertial systems
whose speeds are within the set defined by the expression (1).
The extreme interval values (7) must be
very close in order to preserve detector’s selectivity.
Consequently, this hypothesis asserts –
light is multilateral. The observer could be moving with any speed (from the
interval (1)) in the relation to the source, but every time in relation to him
there will exist some light that has the speed c.
Because of that, there we get the
impression that it is the same light and that its speed does not depend on the
relative speed between the source and the observer.
Naturally, any time it is another light,
in other words it is another spectrum having a different speed in relation to
the source.
If the observer is « measuring »
the speed of light at any given relative speed between him and the source, then
the observer is always « measuring » a speed of detectable light in
his inertial system and he always gets the same value which is natural.
The constancy of light velocity is only
illusion since the light spectra are detectable only when they have the
speed c in their relation to the observer.
GRAPHIC VIEW - REQUIREMENT OF
THE DETECTION
(Detail “A”)
VS – Vr = C
![]()
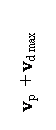
![]()
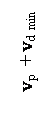

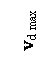
![]()
![]()
![]()
![]()
Pic.
2
The Interpretation of the Michelson’s Experiment
according to
this Hypothesis
The light paths in the legs of the Michelson
interferometer for the moving observer with a speed v, in the relation to the
interferometer, in principle, look like those in the picture 3.
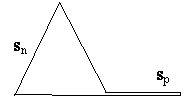
Pic. 3
v v l pi G1 G2 ki v v O3 O4 b![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The light
impulse path with particular length in the normal interferometer leg looks more
detailed in the picture 4.
O1 O1 O2 b Pic. 4

The beginning of the light impulse pi travels
over the path O1G1O3 and the end of the light
impulse travels over the path O2G2O4. This, of
course, by analogy is valid for any elementary part of an impulse. Thus, the
reflected light impulse is normal to the direction of the incoming light and it
has translative speed v in the relation to the observer. Hence, it follows that
the orientation of the light impulse does not coincide with the path direction
of its elementary parts for the observer who is not in the inertial system of
an interferometer.
The
light paths are looking differently in the relation to different inertial
systems, but as it is going to be seen, the light paths in their relation to
interferometer look equal when observed from any inertial system.
a) Interferometer is moving
with a speed v in relation to the referential system
oPr source o Op v Pd l o v
sn c c’ v Ok b
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()

The interferometer and the observer Pd are
moving with the speed v in the relation to the referential system. The observer
Pr and the source are located in the referential system.
Under the 2nd regulation of
the Hypothesis, the spectrum that could be detected in the inertial system of
the interferometer has a speed vs
= c + v in the relation to the
source, and under the 3rd regulation of the Hypothesis, in the
relation to the interferometer the speed is declared as vps= vs – v = c + v – v = c.
With that speed, the spectrum
comes to the semi-permeable mirror and it is reflected at the angle of 90 o toward the direction of that spectrum also with the
speed c (pic. 5). Because the mirror is moving with the speed v, then a
reflected spectrum also moves translatively with that speed, and thus any
elementary part of that spectrum is moving with the total speed c’ = c + v. However, here we should highlight that the spectrum orientation
is normal to the direction vs of
the incoming spectrum after it had been reflected off of the mirror. The
orientation of the reflected spectrum and the direction of movement of
elementary parts of such spectrum are not coinciding for the observer Pr.
The total path of the elementary parts of
spectrum is 2sn = 2 (l2 + b2)1/2
and their speed is c’ = (c2 + v2)1/2 in relation to the referential system. The
time needed for travel of such path is
2× sn v×l
T = ¾¾ , and because
b = ¾¾ then
c’ c
T = 2 [(l2 + v2l2/c2)/(c2
+ v2)]1/2 = 2l/c
It should be taken into the consideration
that the observer Pr
is considering the spectrum that is not electromagnetic for him but for the
observer Pd who is moving along with interferometer.
Obviously, the relative spectrum speed is
not c’ = (c2 + v2)1/2 in relation to the leg of
interferometer but c, because normal leg of the interferometer also has
spectrum’s translative speed v, and thus this component of the spectrum speed in
the relation to the interferometer is equal to zero.This is of course valid for
the path which is not 2sn =
2(l2 + b2)1/2
but 2l, for the component
of the path b is the consequence of the speed v, and this speed in the relation
to the interferometer does not exist, for b = v×l/c = 0.
Thus, light ray’s speed in the relation to
the interferometer equals c, and the path equals 2l for both of the observers.
The time needed for such travel is 2l/c.
Here we should highlight that it is necessary
to observe only what is happening in the relation to the interferometer and not
what is going on in the relation to the whole referential system, so that the
true about this happening will be identical and absolutely independent from the
aspect of the viewing position.
First of all, let’s determine first
spectrum’s path part in the leg of interferometer which is positioned in the
direction of an incoming spectrum. This path part is the path that spectrum
travels from the passage through the semi-permeable mirror to the non-permeable
mirror (pic. 6).
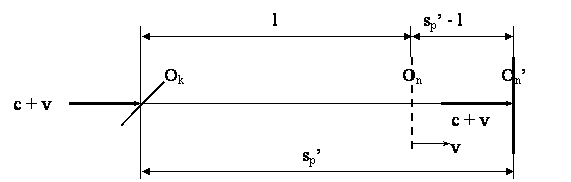
Pic.
6
sp’ sp’ – l
l
sp’ l
After ratio ¾¾¾ = ¾¾¾ it follows
that sp’ = ¾ (c + v) and T1
=
¾¾¾ = ¾
c +
v v
c
c + v c
The second part of the path
that the spectrum travels when reflected from non-permeable towards
semi-permeable mirror is accomplished from the ratio (Pic. 7)
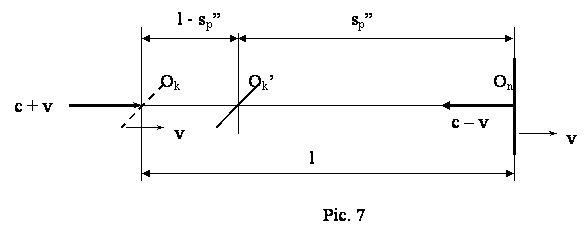
sp’’ l – sp’’ l sp’’ l
¾¾¾¾ = ¾¾¾¾. Hence, sp’’ = ¾ (c – v) and
T2 = ¾¾¾ = ¾
c – v v c c – v c
so the total travel is
sp = sp’
+ sp’’ = l×(c + v) / c + l×(c
– v) / c = 2l
and the total time is
T = T1 + T2
= l / c + l / c = 2×l / c
It could be seen that the spectrum with
speed c + v in relation to the source has both the speeds : c + v, and c – v in relation to
the referential system, but in relation to the interferometer that velocity is
always c.
By accepting this hypothesis, there is no
difficulties with interpretation of the Michelson’s experiment – there is no difference in path
lengths within interferometer, neither there is a time differences, and thus
there could be no interference.
b) Interferometer is within the
referential system
If the source is moving in relation to the
referential system at any speed v, such light spectrum could be detected in the
interferometer that in relation to the source has the speed c + v, for such
spectrum would, according to this hypothesis, have speed c in relation to the
referential system, which is identical to the case when the source was in the
same inertial system as was interferometer. For an observer in referential system,
it is not at all important to know the speed of source movement –
for
him the only important fact is that light’s spectrum (with speed c), the
observer could detect is incoming into the interferometer. Thus, all happening in the interferometer
will be identical and independent from speed of the source.
Because the light paths in the
interferometer legs are also equal, there could be no interference.
The
Experimental Testing of the Hypothesis
Experiment with the source and device located
on the Earth
The first part of the experimental task is
to single one spectrum out of the spectral order which is emitted by the source
(that is practically impossible) ; more exactly the goal is to single out
one interval of spectra as narrow as possible, so we can determine its borders.
In the second part of the task we are
testing interaction possibilities of an already singled out interval of spectra
with a light detection device in various inertial systems.
The experiment consists of the following
elements : light source (i), moving obstacle (Z) with openings (A and B),
immobilized mirror (Os), movable mirrors (Od) and light
detection device (P) . The distance between
moving obstacle and immobilized mirror is marked with l, moving obstacle speed
with w, movable mirrors speed with u, speed of any one spectrum with vs.
The openings’ dimensions A and B are equal, and the meaning of marks h1
and h2 is visible in Picture
8. The moving obstacle with openings represents a spectra group (interval)
separating device. By a way of moving mirrors, various inertial systems are
being accomplished.
It is obvious, from a picture, that
spectra with all speeds in the interval marked borders could go through the
spectra separating device
2 l 2 l
vmin = ¾ w and
vmax = ¾ w
h1 h2
and
more exactly, particular spectrum with
speed vs can go through the spectra separation device only if the
following requirement is met
2
l 2 l
¾ w < vs < ¾ w
h1 h2
That separated interval
comes to the movable mirrors where it is reflected and then reaches light
detection device. According to the Hypothesis, the interaction between
particular spectrum from that interval and light detection device could be
achieved if
vs – 2 u = c
but
more exactly, while the movable mirrors’ speeds are within the interval,
l c l c
¾ w - ¾ < u < ¾ w - ¾
h1 2 h2 2
If we give the speeds outside of such
interval to the movable mirrors by not changing the speed of movable obstacle,
then the interaction of light detection device is not going to be possible with
neither one spectrum from the group that is going through the movable
obstacle’s openings, and more exactly the light belonging to one inertial
system could not be detected from the another
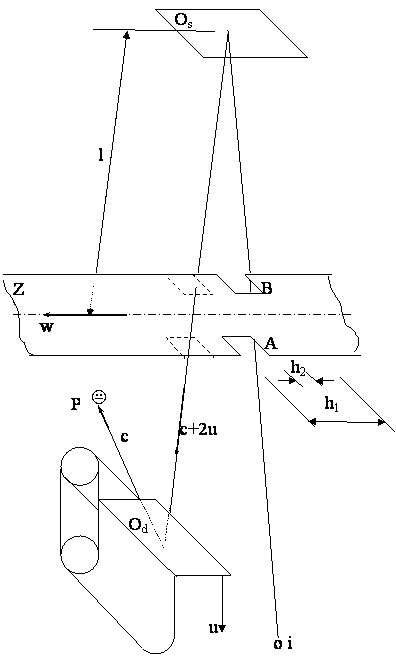
Pic.
8
The Experiment Utilizing the Space Light
Source
The source must be such that
something is happening at it (for exam. Supernova). The information about event
at the source is reflected by any spectrum from the order which such source
emits, thus, the information about the same event travels at various speeds in
the relation to the source and in the relation to the observer on the Earth.
The observer has the option of detecting both the light coming from the source
and the reflected light from the movable mirror which is moving at uniform
velocity u, in the relation to the observer (Pic. 9.).
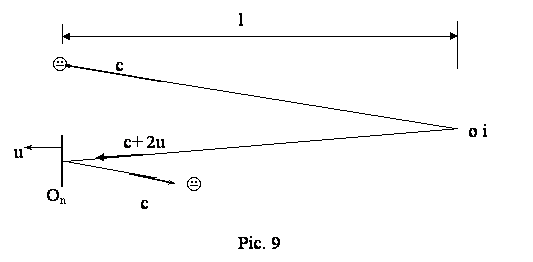
Among the spectra coming from the source,
there is a such with the following speed in the relation to the observer
vs= c + 2 u
Such spectrum has been slowed down by the movable
mirror so the observer could detect it, and it brings the information from the
source earlier than the spectrum with the speed c that is observed directly.
If we mark the distance between the event
location at the source and the observer at the Earth with l, then the arriving
information’s time difference will be
l
l 2 l b
Dt = ¾ - ¾¾¾ = ¾ × ¾¾¾
c c + 2 u c
1 + 2 b
where b = u / c. In such a way, it is possible to detect the event at the
source earlier than when the source is observed directly, if a mirror is moving
in the direction away from the source. By changing the direction of a mirror
movement it is possible to register reprisal of the events after the time
2
l b
Dt = ¾ × ¾¾¾
c 1 –
2 b
in relation to the time when the event was detected
and when source was directly observed.
By knowing
the difference Dt and the movable mirror’s speed, the distance
of the observed space source could be calculated with
c× Dt 1 + 2 b
l = ¾¾ × ¾¾¾¾
2 b
depending on the direction of mirror movement.
The Experiments with Space Sources With the Occurrences of Irregular
Shine Changes
If for a long period of time we follow these changes,
observing the source directly (for example, the change of shine of the γ Cassiopeiae star) and by means of
movable mirrors, only to show them as a separate diagrams, then the same
diagram configuration will be shown in the various times depending on the speed
and the direction of moveable mirrors (Pic. 10.).
Pic.
10
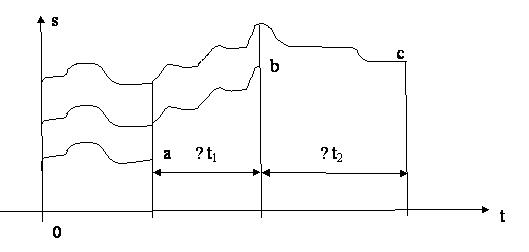
If we
would have three devices drawing shine diagrams at the same time, the device
detecting light directly from the source would at some point draw the diagram
spot b.The device detecting light reflected off of the rotating mirror moving
away from the source would already draw the spot c, while the device detecting
light reflected off of the mirror rotating towards the source would only begin
drawing a spot a. The time, device needs to draw the diagram from the spot a to
the spot b, is ∆t1; and time from the spot b to the spot c we
mark with ∆t2 depending on the mirror’s speed.
This is most likely the cheapest and the
easiest experiment that should be conducted in order to prove the correctness
of this Hypothesis.
CONCLUSION
According to this hypothesis,
it is possible to explain the phenomenon of the speed of light’s constancy, as
it was shown, in a very simple way. This manner differs from the one suggested
by the Special Theory of Relativity. The experiments offered herewith, could
prove beyond the shadow of a doubt, or they could unmistakably refute the
correctness of the one of these two solutions. The dilemma about the correct
solution must not exist, and the only way to eliminate it is by conducting
fundamentally different experiments from those that had already been conducted.
Some of them are suggested herewith.
The results of these
experiments will certainly be against one or the other solution, but that in
fact is not the most important thing – they won’t be against the Science.
I appreciate any and all suggestions,
questions, comments, and notes that have a logical and experimental basis.
Author
Address :
Dane Gacesa
Sestara
Bukumirovic 108 a
BELGRADE
(
E-Mail :
This paper and its
parts are authorized by:
Biro za zaštitu autorskih prava;
Belgrade, No 59/78 – 29. May 1978.
Radna organizacija za zaštitu autorskih
prava “Pronalazaštvo”;
Radna organizacija za zaštitu autorskih
prava “Pronalazaštvo”;
Radna organizacija za zaštitu
autorskih prava “Pronalazaštvo”;
Preduzeće za za zaštitu autorskih
prava i inženjering “Autorski biro”;
Jugoslovenska autorska agencija;
Jugoslovenska autorska agencija;