THE NATURE OF MASS
Mass has been considered a fundemental property of matter ever since Newton invented it in the mid 1600's to account for inertial effects. However it posesses a characteristic that leads one to believe that it is not a fundemental property. The characteristic is that of changing with velocity when placed in an electrostatic field.You would think that a fundemental property would be constant.
If mass is not a fundemental property, then what is it? We know a lot more about matter and atomic structures than in Newton's time and, since objects never actually touch each other (force is transmitted through the electrostatic fields associated with the particles involved), we must assume that mass is the result of some mysterious phenonemon internal to individual particles or mass is the result of external reactions of the particles and the electromagnetic fields of other particles.
A second consideration is the dimensional link to electrostatic charge. If the equation for inertial and electrostatic forces are equated:
![]()
Dimensionally this is:
![]()
and solving for M and Q produces:
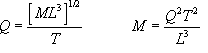
This is an interesting condition. Mass and charge appear to be intimately connected. Either that or they are both functions of other parameters such as length and time. I believe that this is the case and the following development is pointed in that direction.
For the purposes of this argument, free space conditions and the cgs electrostatic system of dimensions is assumed. That is, the dielectric constant (ke) is dimensionless and equal to unity.
Stable matter can be considered to be composed of negative charges (electrons), positive charges (protons) and neutral charges (neutrons). The proton posesses a mass approximately 1836 times that of the electron while the neutron is slightly heavier than a proton. The charges are opposite polarity and essentially equal in magnitude. For the purposes of this development, a neutron will be considered to be a proton and an electron in close proximity although modern physics considers it to be a unique particle. The reason for this assumption will be provided later.
Charged particles are characterized by an electrostatic field which surrounds the spherical particle uniformly in all directions. The field theoretically starts at the surface of the particle and diminishes as the square of the distance from the center of the particle. Several relationships have been established for this field as follows:
Electrostatic force - The force between two point charges is given by:
![]()
The force between two point charges q1 and q2 is directly proportional to the product of the magnitude of the two charges and indirectly proportional to the square of the distance between them. A positive force is one of repulsion. i.e. unlike charges attract and like charges repel. This law was first suggested by Priestly and first published by Coulomb in 1770.
Electric Intensity (field strength) - The force exerted on a small positive test charge held at rest in any position or point in an electrostatic field divided by the charge is called the intensity (field strength) at that point:
![]()
The force on a charged particle at any point in any field configuration (square law, linear or otherwise) is:
![]()
and is in the direction of the field strength at that point.
Electrostatic Potential - The electrostatic potential at a point in an electrostatic system is defined as the work done in bringing a unit (positive) charge from infinity up to the point:
![]()
It is to be noted that:
![]()
The concept of mass was first introduced by Newton in 1687 to account for inertial and gravitational effects of gross matter.
For inertial effects, a mass (m) is accellerated (a) by applying a given force (f) such that:
![]()
For gravitational effects, the force between two masses (m1 and m2) is equal to a constant multiplier (G) multiplied by the product of their masses and divided by the square of the distance between them. A positive force is one of attraction.
![]()
It was subsequently shown that that inertial and gravitational masses were equal.
Within our present understanding of atomic and molecular processes, force is never directly applied between objects. At the atomic level, individual particles are arranged in a specific stable manner with respect to each other and the group moves as a whole. Forces between these individual particles are transmitted through the electromagnetic fields that comprise their structure. At the molecular level, individual atoms that make up the molecule are tied together through the electromagnetic fields associated with the shared electrons. Gross matter is comprised of some combination of molecules and again force between individual objects is transmitted through the electromagnetic fields associated with the outermost electrons at the molecular level interface.
Another effect that indicates the electromagnetic basis of mass is the apparent increase in mass with velocity as the velocity of the mass increases with respect to the velocity of propegation of the medium through which it traverses. This is at least true for masses associated with charged particles which are subject to force through electromagnetic fields. If we rewrite the basic inertial equation such that:
![]()
we find that, for mass to increase with velocity, the accelleration must decrease since the force associated with the field is considered to remain constant. It should also be noted that, if force is described in electrical parameters, accelleration should also be able to be described in electrical parameters since their ratio is independant of electrical parameters.
In its simplest form,we can investigate the accelleration of a single charged particle in a linear field where the force is:
![]()
Here E1 is the strength of the field and q2 is the magnitude of the charge. The following model is proposed.
A single charged particle suspended in free space, which is not under the influance of any other field, posesses an electrostatic field which is completely symmetrical about it and there is a zero net force applied to the particle. A test charge brought in from infinity will show the same force vector which is normal to the surface of the particle regardless of the direction of approach.
If we now introduce the particle into a linear electrostatic field, the lines of force will be distorted such that the resultant force vector becomes other than zero and is directed in the direction of the accellerating field. As a result, the particle moves in a direction which tends to return the lines of force to the free space conditions. The following actions are deemed to contribute to the accelleration of the particle.
1) The accelleration will be directly proportional to the strength of the linear field, which controls the magnitude of the distortion of the particles field.
2) The accelleration will be directly proportional to the ability of the particles field to recover to its free space condition. This can be likened to a spring function. It is proposed that this function (S) is proportional to the rate of change of field strength.
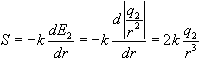
At the surface of the particle the value S is:
![]()
This indicates that S is proportional to charge density of the particle. S is not to be confused with the divergance of the induction vector (divD) even they are both proportional to charge density under certain circumstances. S is finite for values of r equal to or greater than ro, while divD is 0 for values of r greater than ro and proportional to charge density at the surface and within the particle.
3) The ability of the linear field to distort the field of the particle will be a function of the relative velocity of the particle with respect to the velocity of propegation of the linear field. When the particle velocity is zero, maximum distortion will occur. When the particle is travelling at the velocity of propegation of the linear field, the particle will act as though it were in free space since interaction between the particle and the linear field can never take place. This effect follows the relativistic transform:
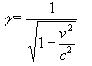
Combining these effects provides an expression for accelleration:
![]()
Notice that the equation for accelleration is independant of mass.
Letting
![]()
(dimensionless, since k is dimensionless) and substituting the resultant expression for accelleration into the basic inertial equation produces:
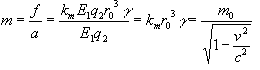
Here the rest mass of the particle is:
![]()
The constant km is recognized as mass density and is dimensionless resulting in mass posessing the dimensions of
![]()
This is consistant with the fact that, under identical environmental conditions, the mass of any matter is directly proportional to its volume. At the basic particle level, since all stable matter is made up of identical electrons and protons, there is no need for mass density to be anything but dimensionless. Here mass density is a measure of the volume of free space contained within the confines of the particle.