ATOMIC STRUCTURES & QUANTUM MECHANICS
Quantum Mechanics predicts energy levels for the stationary states of atomic structures but it gives no clue as to why they should exist. The energy states are supposedly related to conditions of quantized momentum. However, in an atomic structure with many protons and electrons, all of the protons appear to be able to maintain close relationships without posessing motion which momentum requires. The same is true with orbital electrons which appear to be locked into a grid of stationary conditions with respect to the protons and each other without having any apparent motion. It seems obvious that these energy states correspond to conditions with zero force between particles. This implies that either other forces are in operation or that the Coulomb force exhibits different properties at the atomic level than it does at greater distances.
The S-S concept provides a mechanism for the quantum states of the atomic structures. Inasmuch as the source and sink are dynamic quantities, they should produce resonant interaction at close ranges that is not apparent an normal ranges of experiment. These resonant interactions can produce zero force conditions at certain ranges with the force between the particles alternating between attraction and repulsion in between.
Let us assume for the time being that the Coulomb force is modified to produce these regions of zero force. One way that this can occur is if the equation is subject to a sine or cosine function. The general condition would be that of a complex exponential function such that:
![]()
For direct functions of r, fq will show signs of an oscillatory nature for large values of r. This has not been observed as far as known. Assuming the inverse function of r and letting ra equal the separation between particles where the force first becomes zero as r gets smaller produces the equation:
![]()
It is understood that ra will be different for electron-proton, electron-electron and proton-proton interactions. It is also understood that the actual complex equation will probably be more complicated than the simple form indicated here. This approach has been used to illustrate the possibility of a mechanism for quantum states, not a specific solution.
Letting ra = ro for an electron-proton interaction:
![]()
Figures 1 through 3 show the real part of this force equation which has been normalized to:
![]()
In the figures, aj is the normalized force function fn, bj is the normalized Coulomb force function and rj is the normalized range (r/ro) which has been plotted in a logrithmic scale to increase visability. Figure 1 shows the functions for normalized range values of 1 to 10 while Figures 2 and 3 show functions for normalized range values of 0.1 to 1 and 0.01 to 0.1 respectively.
Figure 1
Normalized range = 1 to
10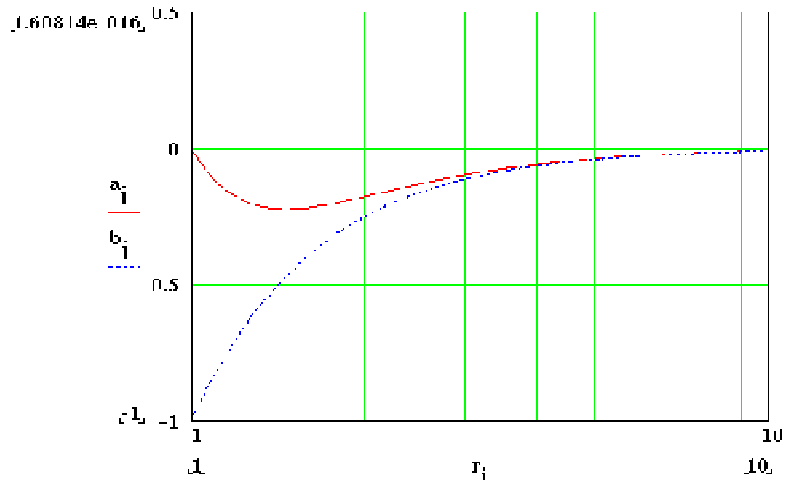
Figure 2
Normalized range = 0.1 to
1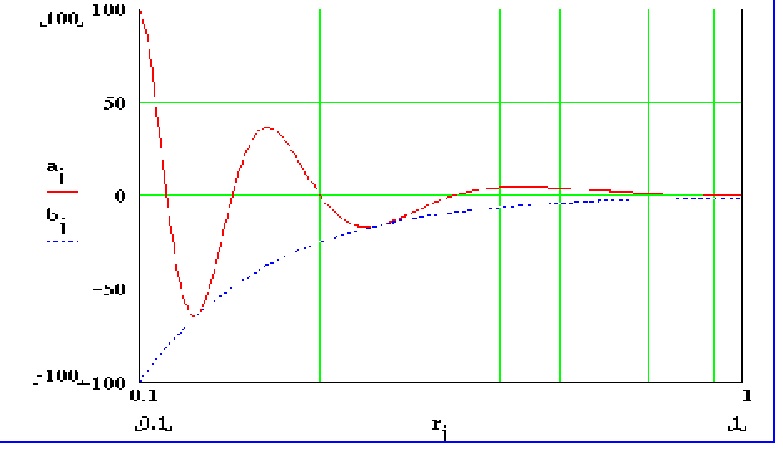
Figure 3
Normalized range = 0.01 to
0.1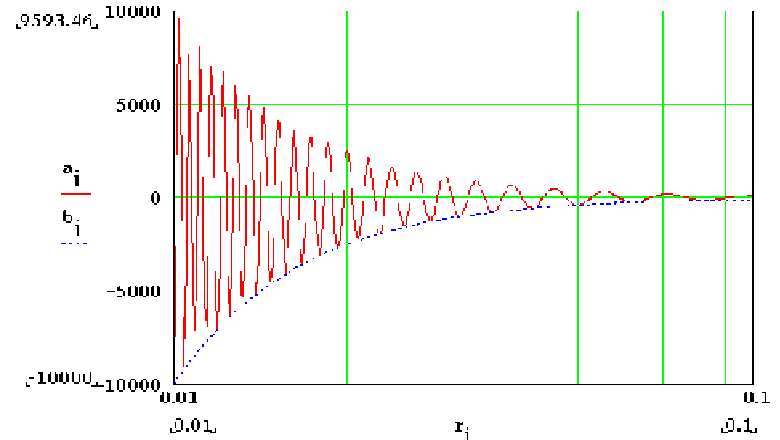
Noting that a negative force is one of attraction, stable zero force conditions occur at ro/r values of 1, 5, 9, 13 etc. and unstable force conditions occur at ro/r values of 3, 7, 11, 15 etc. A stable force condition is one where an increase in r causes an attractive force while a decrease in r results in a repulsive force, thus it takes additional work to displace the electron with respect to the proton in either direction.
If we let n equal the values of ro/r where the force is a stable zero, we find that ro/r = 4×n - 3. For n greater than 1, the peak maximum attraction is at values of ro/r = 4×n and the peak maximum repulsion is at values of ro/r = 4×n - 2 as shown in Figure 4.
Figure 4
Electron-Proton force
relationships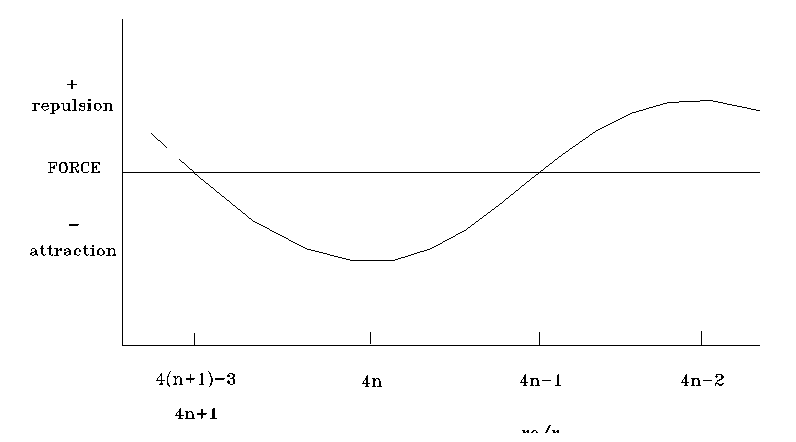
It needs to be understood that the equation cannot proceed to infinitely small values of r since a point will eventually be reached where the electron and proton can no longer be brought closer together due to the finite size limits of the particles. However, since we do not know the exact sizes of the basic particles, this point cannot be accurately predicted. In all reality, the equation would have to be modified to account for the physical sizes of the particles as they come within close range of each other.
The electron and proton are envisioned to act as follows as the two are brought together from infinite range. Between the ranges of infinity and r/ro = 1, the force is attractive naturally and no external energy need be added to the system. The system is actually providing the energy required since, theoretically, external energy had to be applied to the system to remove the electron from its stable position at r = ro. The energy of the system at separation r is given by the negative of the integral of force vs distance. i.e.
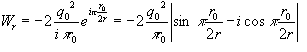
The energy required to remove an electron from the hydrogen atom is 13,530 electron-volts or 2.1528×10^-11 ergs and the electron charge is 4.80325×10^-10 esu. Consequently, ro is equal to 0.682255×10^-8 cm (0.682255 Angstrom units)
It will also be noted that, for large values of r, the real part of the energy equation reduces to the familiar one since sin(a) approaches a as r becomes large:
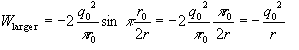
At r = infinity, the energy stored in the field is:
![]()
This is the amount of energy added to the system to remove the electron to infinity.
An interesting relationship exists between the amount of energy required to move the electron between positions of neutral stable force (4×n - 3) and positions of unstable force (4×n - 1). As the peak force increases with n, the distance decreases and the net result is that it takes the same amount of energy to make the transition no matter what the value of n. i.e.
![]()
and the energy returned to the system in moving the electron from the point of neutral unstable force (4×n - 1) to the next point of stable force (4×n + 1) is:
![]()
A possible explanation for quantum states has been show. However, what about all of the special so called "fundemental" particles which have arisen out of high energy physics experiments. First, these particles have a life span in the order of 10 nanoseconds (0.00000001 sec). A truly fundemental particle ought to last longer. Electrons and protons do. Secondly, high energy experiments are basically destructive in nature. If we consider the basic atomic structures to be held together by resonant fields, then the whole structure will posess resonant responses to outside disruptions. If the structure is bombarded with particles at just the right velocity, severe vibrational conditions can be set up which temporarily disrupt the stable structure. I believe this to be the case. We have elaborate theories to explain how all these "fundemental" particles fit together in a master jig saw puzzle. One of the latest is Superstring Theory which requires 10 dimensions in which matter exists. These theories are necessary because of the insistance that the fragments of high energy bombardment are real particles. The approach has been promoted so long and hard that it is nearly impossible to give it up and accept that the byproducts are no more than what they really are. Distructive debris.
As a side issue, the S-S concept can explain why a stream of charged particles produce interferance patterns similar to that produced by a light beam passing through narrow slits. It even explains why the diffraction pattern is produced with a single slit and probably could be produced with a single edge. Since the force between charged particles varies cyclically with separation, the charged particles will react differently with the outermost electrons on the edge of a slit. Since the beam does not consist of a single line of particles, the particles will pass the edge at varying distances. Some will pass straight through if the separation is right for a null force zone, some will be deflected away in one direction with varying degrees of deflection and others will be deflected in varying degrees in the other direction. since there are multiple separations where a null zone can exist, this process is repeated at successive distances from the edge. The net result is that interferance patterns will appear on a target area past the slit. The wave effect associated with particles is not associated with the individual particle, but rather as an effect between particles.